日寄 of March,2025

3.1

教练给我们做综合训练了，专题会停一段时间吧。

早上发了 6 道 DP 题，做了两道。

教练让我们写总结了，但是我并不想把这个发过去，因为我可以在这里发电太懒得 push 了。

3.2 - 3.4

忘带硬盘了，所以没写，放一起吧。

3.2 晚上打了 EUC 的 OM，一道没切，然后就没有然后了。

3.3 是做题，教练抓了 EUC 和 ASC 的题，只能看题解做点简单的了，我太菜了。

3.4 考试。

T1

考虑每一条边对答案的贡献，我们可以大胆猜测，这条边会产生 $2 w \min \{ sz _ u,sz _ v\}$ 的贡献，因为小的子树可以连向大的子树，每条路径都会产生贡献。

因此，答案就是 $2 \sum \min \{sz _ u,sz _ v\}$。

T2

神仙结论题，但我按计算几何的方式思考的。

先说结论，$Ans = \frac{n - 4}{2}$，多边形内角和为 $180 \degree(n - 2)$，设 $270 \degree$ 的角有 $x$ 个，则 $90 \degree$ 的角有 $n - x$ 个，则有

但是，我就不一样了，我本来想用向量叉乘的，但是懒得写高精度了，于是使用了分类讨论大法。

虽然 $\Omicron(1) \to \Omicron(n),10 min \to 2h$。

T3

首先，我们考虑下面的平行四边形。

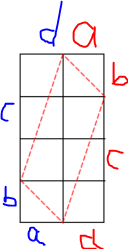
红色部分可以通过全等证明。上高中了初二的东西还在追我

则平行四边形的面积为 $(a + d)(b + c) - (ab + cd) = ac + bd$，则 $f(p) = \sum [ac + bd = p]$。

我们考虑方程 $ab = p$ 的解的组数，等于 $p$ 的正因子个数，记为 $d(p)$，设 $i = ac$，则 $bd = p - i$。则 $f(p) = \sum _ {i = 0} ^ p d(i) d(p - i)$。

直接计算是 $\Omicron(n ^ 2)$ 的，过不去，考虑优化。发现这个式子长的就是个卷积的形式，于是，我们可以先预处理出 $d(x)$，然后用 NTT 优化卷积，最后套个 RMQ 就解决了。

时间复杂度：$\Omicron(V \ln V)$ 的预处理，$\Omicron(V \log V)$ 的 NTT，$\Omicron(t \log V)$ 的 RMQ，可以通过此题。

T4

不会。

3.5

综合训练，只做了一道题，寄。

懒得写题解了。

3.6

考试。

赛时估的是 125pts，但是 T1 我【数据删除】的把 Lf 打成 lf 了，痛挂 20pts。

T2 DP 是想对了，但是没有限制子串长度，100pts → 50pts。关键是赛场上拍了 2000 组愣是没有找到 Hack，我【数据删除】的数据。

电发完了，下面是题解。

T1

我们设 $dp _ {i,j}$ 表示有 $i$ 条同色链，$j$ 条异色链的期望连通块数，则有转移：

T2

我们设 $dp _ {i,j}$ 表示考虑前 $i$ 项，长度为 $2j$ 的答案，用 pair 存起来。

转移非常简单，$dp _ {i,j} = \max \{dp _ {i - 1,j},\text{Merge}(dp _ {i - 1,j - 1},s _ i,t _ i)\}$，则答案为 $\max \{ dp _ {n,i}\}$。

需要注意，我们需要钦定一个长度，不然会爆炸。

T3

没改。

T4

没改，发现如果全空则答案为 $n + m - 1$，悲提 40 pts，因为赛后才注意到。

3.7

今天补概率与期望 DP，同时改了个高斯消元的板子。

最糖的一集

3.10

3.8 的改题去了，不想写了。

今天是 DP 专题。

3.11

今天 VP CF Div.2。

思维没有打开，AB 都在 20min 内切了，但是 C 第一次想的构造炸了，心态也跟着炸了。所以导致只做了 $2$ 道题。

其实我应该是可以想出 E 的构造的，但是心态炸了 /

然后就去写概率与期望了。

本来晚上是想打 Div.3 的现场赛的，但是玩战地去了，明天早上打 VP 得了。

3.12

VP Div.3

A

唐题，判断是否 $L = R = U = D$ 即可。

B

根据样例解释做题，选择两个最小的，然后新的一定比原来的大，这样连环套的只剩一个的时候答案最优。

C

转化式子，题目让我们求的是 $x + y \gt x \oplus y \gt x - y$ 的 $y$，再从异或的性质入手，继续转化为 $x \operatorname{and} y \neq 0 \wedge x \operatorname{and} y \neq y$，删去最高位，加上最低位就能了。

D

我们发现 $m$ 小的可怜，于是从这里入手。通过数学，我们可以求得，直线 $x = k$ 在圆 $x ^ 2 + y ^ 2 = r ^ 2$ 上/内部有 $\lfloor \sqrt{r ^ 2 - k ^ 2} \rfloor$ 个整点，然后直接扫一遍，如果有更大的答案更新即可。

E

神仙构造题，我们首先随便问一个 $\triangle ABC$，极大的可能会返回一个 $P$，通过直觉推断，将一个点换为 $P$，里面的点会变少。

然后，就没有然后了，似乎只能推出这么多。

我们先来详细证明一下：

设 $\triangle ABC$ 中有 $c$ 个点，$\triangle APC$ 中有 $c _ 1$ 个，$\triangle PBC$ 中有 $c _ 2$ 个，$\triangle ABP$ 中有 $c _ 3$ 个，则 $c _ 1 + c _ 2 + c _ 3 + 1 = c$。

根据鸽巢原理，至少有一个 $c _ i \ge \frac{c - 1}{3}$，则我们可以随机的把 $A,B,C$ 其中一个替换为 $P$，随机到最少的那个的概率是 $\frac{1}{3}$ 的，因此，只要多随机几遍，我们就能得到一个 $c = 0$ 的三角形。

我不会证，但是期望次数是 $7$ 次左右，远小于 $75$。

后悔晚上没打这场了 $qwq$。

然后概期有一道题，可以用 DDP 做，就想去学。DDP 是没学会，但是找到了一些矩乘线段树的水题。

3.13

今天考试，总结来说，就是策略没设计好还有出题人戶口本（輕量化）。

T1

看到题就觉得肯定极其难写，发现第一个点 $r \lt 100$，而样例给的是 $[1,135]$，复制即可。

T2

和期望其实没什么关系的期望题。

赛场上看到级数懵了，推了两个多小时的式子，然后发现假了，就开始打表，发现 $n = 2,m = 2$ 的性质，然后算错了，痛失 $10$ 分。

我打表的时候，发现如果有连续的，答案会和没有连续的答案不一样.然后没有想出更多的性质了。

实际上，答案是 $m ^ n + \sum _ {p \in \text{Border}(B)} m ^ p$。

那这样就很简单了，跑一遍 KMP，然后 i = n 后一直 i = next[i] 就是了。

T3

和哈希的题，在赛场上口胡了一个类似莫队的做法，成功没挂 $40$，其实出题人把 $m$ 开到 $\frac{n}{\log n}$ 我就能过，但是他显然没有。

正解是首先统计出前缀权值数组 $V _ i$，然后 $[l,r]$ 合法的充要条件显然是 $V _ r - V _ {l - 1}$ 的每个值相等。我们可以差分每一个 $V _ i$，记为 $C _ i$，则每次修改完，我们就查询有多少个 $\text{Hash}(C _ j) = \text{Hash}(C _ i)$，计入答案即可。

注意哈希函数要设计为 $f(-x) = -f(x)$，即一个奇函数的形式。

T4

定位是签到题，但是出题人倒序放题，发现 $u$ 与 $2u,2u + 1$ 有依赖关系，考虑建树。然后就是一个简单到极致的树形 DP。

总结

1. 不要死磕（写几遍了）
2. 正着做不动倒着做

3.14

综合题。

数论的东西也缺。

3.15

考试。

T1

哇原来我还能场切题啊

首先口胡一个结论，对于一个位置 $i$，所有包含它的区间设为 $w$，其余全部设为 $0$。

严格证明不会，你就想，如果区间内有比它大的，你加的少和加的多都没用，该追不上还是追不上，但是加的多更有机会追上区间外比它大的。

所以，我们可以扫描线过去，遇到一个区间的开始区间加上 $w$，遇到结束的后一个位置减去 $w$，线段树维护即可，每次单点求值，判断是否与全局最大值相等。

T2

考虑树形 DP，观察到根是否能 AC 只跟根所在的连通块大小有关，则可以用 DP 来求。

设 $dp _ {u,i,0/1}$ 表示以 $u$ 为根的子树，给 $i$ 个点提交，$u$ 是否过的概率，发现不好转移，则我们再设一个 $g _ {u,i,0/1}$，表示不包含 $u$，提交了 $i$ 个点，$u$ 的儿子是否过的概率，则我们先转移 $g$，然后用 $g$ 的值转移 $dp$。

然后在转移的时候，我们建立一个 $tmp$ 表示新的 $g$（因为我们需要 $g$ 原来的值），则 $tmp _ {i + j,k \vee t} \gets tmp _ {i + j,k \vee t} + C _ {i + j} ^ j dp _ {v,i,k} g _ {u,j,t}$，更新完以后，$g _ {u,i,0/1} \gets tmp _ {i,0/1}$，然后拿去更新 $dp$，$dp _ {u,i,0} \gets g _ {u,i,0} + g _ {u,i,1},dp _ {u,i + 1,0} \gets \frac{1}{2}g _ {u,i,0},dp _ {u,i + 1,1} \gets \frac{1}{2} g _ {u,i,0} + g _ {u,i,1}$ 就好了。

T3

什么神奇题没改。

T4

赛场上一个假的不能再假的做法，还骗了 $72$ 虽然在赛后被卡成 16 了就是。

我们考虑钦定 $l$ 是最大值，$r$ 是最小值，则满足条件的 $l$ 一定在 $[pre + 1,r]$ 上，其中 $pre = \max _ {j \lt i,a _ j \lt a _ i} j$，如何确保 $l$ 最大？我们可以直接建一个单调栈，把 $[1,i]$ 中的元素加进 DS 里面，查询异或极值就好了。

那么用什么 DS 呢？我们需要区间查询异或极值，则直接用线段树套 01Trie 就是了。

3.17

自习。

因为周六的一场 Div.2 因为 Mike 在玩原神 CF 服务器抽风没打，所以就直接去补题了。

感觉这场 Div.2 比之前打过的都难，B 题都 1500。

然后就是回去补可持久化专题了，嘿嘿该我玩了。

今晚打了 Edu，起码没有掉分。

经典过 AC 不过 B。

我突然发现我有个 Cnblogs 的账号，于是我决定把题解全部甩到那上面去。

题解链接↗

学习笔记和日记会留在这个网站上的，不然我这个网站就没意义了。

3.18 - 3.19

感冒发烧了，回家了，打了一天 BF，3.20 回来了。

3.20

回来了，看见 lx 把我刷下去了，直接翻出我的陈年提交记录~~（坏笑）~~

然后交完一看，欸，zcy 还有比我更早的，zcy 得了 MVP $\uparrow$。

中午把之前一个被卡空间的树套树重新写了一遍。

准备加个像 LOJ 一样的一言，但是这个工程量有点大，慢慢来吧。

3.21

今天考试，挂了 24 分。

题解↗

只能说思维还是不太行，构造还是太劣了。

图论算法都会，就是不会建图。

3.24

昨天晚上教练叫我们去打了 ARC，但是我去补主席树了，就没好好打。

反正今天还是得补题，还有周末的两场 Div.2 的题。

还有我发现我非常擅长把简单的问题复杂化。

明天要模拟体测，还好是在上午。

3.25

真的很烦这种临时变卦的老师，第一节课本来说自愿体测，去自由活动了 20min 就把我们抓回来体测，体测就立定跳远还能看，机房残疾人果然不是吹的。

然后回来做 DP，升难度了，到了 $2100 \sim 2400$，但是有道 1900 的，这个我会，我也只会这个了。

Solution Link↗

下午开了线性基的专题，先把模板题过了。

3.26

考试，挂了 15pts。究其原因是我 T3 记录答案的时候没有初始化。

Solution Link↗

下午和 T3 斗智斗勇，然后炸了。看来 DP 还是太弱了。

3.27

又是 DP 综合，但是今天居然做了三道题。

Solution Link↗

线性基的专题还有两道就做完了，因为八纵八横需要可删除线性基，我又懒得去学所以就写了线段树分治。

J 题需要前缀线性基，考虑不学，使用 lxl ST 表诶嘿嘿。

3.28

呜呜呜今天综合训练一道没切。

有一道原题，但是完全没有思路。

今天事情太多了没写题解，那直接不写得了。还有今天晚饭是真的难吃，幸好还有桶泡面。

明天说是 S 组难度的涨信心模拟赛，看吧。

3.29

还真是涨信心模拟赛，我还能考 224，不挂分还能考 259。

因为题太唐了，也太恶心了，所以不单独写题解了。

T1

纯唐数论题，筛出 $[1,10 ^ 6]$ 的质数就能求出来了。

T2

大模拟，但是出乎意料的好写。

T3

拿高考数学 20 题改的，结论比较难猜，但是猜出来就很简单。

T4

假期望真数位 DP，太恶心了不改。

3.31

今天拉的是比较简单的一套综合。

Solution Link↗

除了后面两道神经 DP 其他的我还挺喜欢的。

啊三月份还是有长进的，起码我能自己做 2100 的 DP 题了吧。

蒟蒻时的 DP 债还得慢慢还呢，四月份加油吧。

Thanks for reading!

日寄 of March,2025

2025 3月 01 周六

5168 字 · 20 分钟

OI生涯记录 日寄 OI

---

© xguagua | CC BY-NC-SA 4.0

分享

分享这篇博客

X (Twitter) Telegram Reddit Facebook Email

关闭

关闭