0.适用场景
转移式形如 dpi=aibj+ci+dj 的 DP 就可以使用斜率优化,因为 aibj 这一项,单调队列优化不再适用。
1.原理
设有转移方程 dpi=minj<i{dpj+(sumi−sumj+i−j−1−L)2},时间复杂度为 O(n2),考虑优化。
先设 Si=sumi+1,l=L+1,为方便,我们先省去 min 的上下界,则有:
dpi=min{dpj+(Si−Sj−l)2}⇒dpi−(Si−l)2=min{dpj+Sj2+2Sj(l−Si)}这个时候我们联想一次函数的解析式 y=kx+b,变形得到 b=y−kx,如果我们把每一个都看作变量,则 kx 是一个二元函数,这启发我们将和 i,j 同时相关的设为 kx,只和一个变量相关的看作 y,b,一般我们设需要取最值的为 b,也就是只与 i 相关的设为 b,则只和 j 相关的设为 y。
又因为我们需要已知斜率,所以 k 为二次项中与 i 相关的,x 为二次项中与 j 相关的。并且,解析式为 b=y−kx,所以一般 k 值需要取负。
在本题中,我们可以做如下变量代换:
b=dpi−(Si−l)2y=dpj+Sj2k=−2(l−Si)x=Sj我们再将 (x,y) 看作平面上的一个点,则题目转化为已知 ki,求最小的 xj,yj,使得 bi 最小。
借用 OI-Wiki 的一张图:
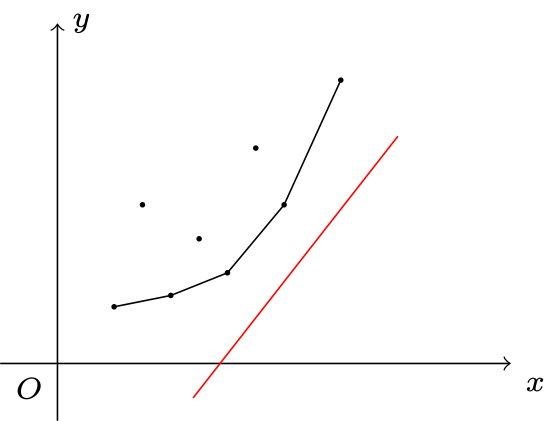
可以发现,我们要做的就是沿着 y 轴从下向上平移这条直线,使得第一个 (xj,yj) 在该条直线上,这时 bi 最小。同时,我们需要维护先前的决策点点集,并且我们发现,这个点集构成一个凸包,分如下情况讨论:
1.斜率与横坐标均单调
我们维护一个队列 Q,使得 ∀i∈(head,tail),Slope(Qi−1,Qi)<Slope(Qi,Qi+1),这里的 Slope 表示斜率。
当我们找答案的时候,就是找到一个点 p,使得 Slope(Qp−1,Qp)≤k<Slope(Qp,Qp+1),此时,点 Qp 就为最优决策点。
我们查询完答案后,我们首先要维护斜率的单调性,我们要使 Slope(Qtail−1,Qtail)<Slope(Qtail,i),弹出所有不满足的 Qtail,再插入这个点,就好了。
2.有不单调的
这个时候就不满足单调队列的性质了,我们可以采取以下方法来维护这个凸包
弹队首变为找到一个最小的 p 使得上面的式子成立,可以用二分实现。
对于插入操作就不那么好维护了,我们可以使用两种方法维护这个凸包:
(1) 平衡树
我们直接用平衡树来维护这个凸包,上面的二分操作就可以在平衡树上二分了。
可以不用手写,直接用 set 就行
(2) CDQ 分治
我不会,看 OI-Wiki 得了↗
2.更高阶的
我们发现,其实我们没必要对式子变形。
我们重新看原来的方程:
dpi=min{dpj+Sj2+2Sj(l−Si)}+(Si−l)2发现,我们的瓶颈就是在求 min 里面的式子。
我们沿用一次函数的模型来解决。但这次,我们的变量代换就不太一样了。
我们沿用二次项是与 i,j 都有关的思路,但是,我们考虑代入求值。则与 i 有关的是已知的,设为 x,与 j 有关的设为 j,min 中只与 j 有关的设为 b,则变量代换如下:
x=Sik=−2Sjb=dpj+2lSjy=dpi−(Si−l)2则问题转变为求一些一次函数在 x=Si 处的极值,同时支持插入线段,这个可以用李超线段树来方便的维护。
并且代码比平衡树与 CDQ 分治短得多
DP总结(四,斜率优化DP)
2025 1月 10 周五 1168 字 · 5 分钟
