数据结构Part 1

0.树状数组

`lowbit` 运算

定义一个二进制数 $x$ 最低位的 $1$ 与后面的 $0$ 组成的 $100 \ldots 0$ 为 $lowbit(x)$ 。

其求法为 $x \& -x$

树状数组

树状数组每个结点维护的是原数组的一段和（不一定是加法的和），先看一张图：

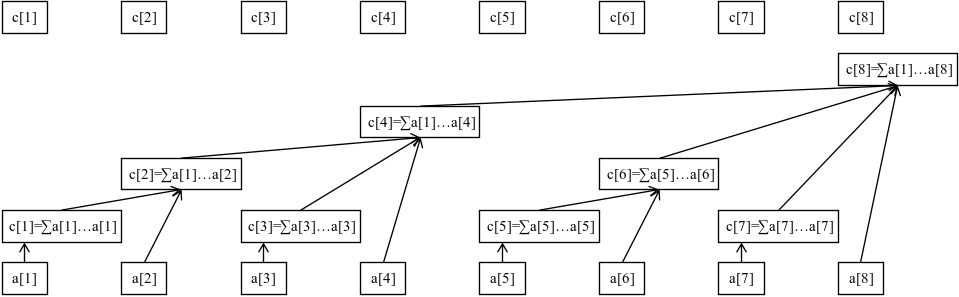
这张图就是树状数组一个结点维护的和。

那到底怎么维护的呢？实际上， $c _ x$ 维护的是 $[a _ {x - lowbit(x) + 1},a _ x]$ 的信息。

区间查询

我们发现， $[a _ 1,a _ x]$ 的前缀和可以在树状数组上在 $\Omicron(\log x)$ 的复杂度内得出。因为我们可以把其拆成几段，然后用树状数组求出。

比如 $7 = 111 _ {(2)}$ ，所以我们可以将 $\sum _ {i = 1} ^ 7 a _ i$ 拆成 $c _ 7 + c _ 6 + c _ 4$ 。此时，我们可以发现，下标每次都是减去了其的 lowbit 值，所以我们可以这么写：

1
inline int query(int pos)
2
{
3
    int res = 0;
4
    for(int i = pos;i;i -= lowbit(i))
5
        res += c[i];
6
    return res;
7
}
8
#define seqQuery(l,r) (query(r) - query(l - 1))

然后这个查出来就是 $\sum _ {i = 1} ^ {pos} a _ i$ 。

所以任意的 $[l,r]$ 就可以通过查询 $[1,r] - [1,l - 1]$ 得出。

单点修改

前面说了，树状数组维护的是一段区间。所以单点修改需要对涉及的区间全部修改一下。

又因为每次都是按 lowbit 值来跳，所以很容易的就可以得出代码。

1
inline void modify(int pos,int x)
2
{
3
    for(int i = pos;i <= n;i++)
4
        c[i] += x;
5
}

区间修改

这个需要结合差分的知识。

因为 $\sum _ {i = 1} ^ {n} a _ i= \sum _ {i = 1} ^ n \sum _ {j = 1} ^ id _ j = \sum _ {i = 1} ^ n d _ i \times (n + 1) - \sum _ {i = 1} ^ n d _ i \times i$

所以我们可以维护两个树状数组，分别维护 $d _ i$ 与 $d _ i \times i$ 。

区间修改时，我们先对 ${c _ 1} _ l$ 加上 $k$ , ${c _ 1} _ {r + 1}$ 减去 $k$ ，再对 ${c _ 2} _ l$ 加上 $k \times l$ ， ${c _ 2} _ {r + 1}$ 减去 $k \times (r + 1)$ ，这样就好了。

代码如下

1
inline void modify(int pos,int k)
2
{
3
    for(int i = pos;i <= n;i += lowbit(i)) //a[1...pos] += k
4
        c1[i] += k,c2[i] += pos * k;
5
}
6
inline int query(int pos) //a[1]...a[pos]
7
{
8
    int res = 0;
9
    for(int i = pos;i;i -= lowbit(i))
10
        res += (i + 1) * c[i] - c2[i];
11
    return res;
12
}

复杂度

空间复杂度 $\Theta (n)$ ，时间复杂度 $\Theta(\log n)$ ，并且常数大大优于线段树，码量大大少于线段树。

实质

就像线段树维护的是一个幺半群，树状数组同理，事实上，树状数组可维护的信息是线段树的子集。

所以，树状数组也可以维护 $\gcd,\max,$ 乘法等信息。

二维树状数组

别名树状数组套树状数组。

对于每行的树状数组，就是一个一维树状数组。

然后，外层的树状数组管辖区间是一致的。

二维差分

$d _ {i,j} = a _ {i,j} - a _ {i - 1,j} - a_ {i,j - 1} + a _ {i - 1,j - 1}$

对于一个子矩阵的修改，相当于 $d _ {a,b},d _ {c + 1,d + 1} += v,d _ {c + 1,d},d _ {a,b + 1} -= v$ （记忆方法：右下角一定加一，然后错排）

又因为有 $\sum _ {i = 1} ^ n \sum _ {j = 1} ^ m a _ {i,j} = \sum _ i \sum _ j \sum ^ i _ {x = 1} \sum ^ j _ {y = 1} d _ {x,y} = \sum _ i \sum _ j d _ {i,j} \times (xy + x + y + 1 - i(y + 1) - j(x + 1) + ij)$

所以可以考虑维护四个树状数组（我真 tm 不想写），来求子矩阵和。

1
#define lowbit(x) (x & -x)
2
inline void add(int x,int y,int val)
3
{
4
    for(int i = x;i <= n;i += lowbit(i))
5
    {
6
        for(int j = y;j <= m;j += lowbit(j))
7
        {
8
            c1[i][j] += val;
9
            c2[i][j] += val * x;
10
            c3[i][j] += val * y;
11
            c4[i][j] += val * x * y;
12
        }
13
    }
14
}
15
inline void modify(int a,int b,int c,int d,int val)
16
{
17
    add(a,b,val);
18
    add(a,d + 1,-val);
19
    add(c + 1,b,-val);
20
    add(c + 1,d + 1,val);
21
}
22
inline int pre_query(int x,int y)
23
{
24
    int res = 0;
25
    for(int i = x;i;i -= lowbit(i))
26
    {
27
        for(int j = y;j;j -= lowbit(j))
28
            res += (x + 1) * (y + 1) * c1[i][j] - (y + 1) * c2[i][j] - (x + 1) * c3[i][j] + c4[i][j];
29
    }
30
    return res;
31
}
32

33
inline int query(int a,int b,int c,int d)
34
{
35
    return pre_query(c,d) - pre_query(c,b - 1) - pre_query(a - 1,d) + pre_query(a - 1,b - 1);
36
}

权值树状数组

这个东西可以解决全局 $k$ 小值，二维偏序问题

其实就是对权值数组建树状数组，然后就好了。

关于逆序对，可以枚举 $i \gets [n,1]$ ，然后求权值的前缀和， $k$ 小值就是枚举 $i \gets [\log _ 2 x,0]$ ，然后每次查询前缀和，若 $sum + [x + 1,x + 2 ^ i] \lt k$ 则扩展，最后 $x + 1$ 即为答案。

然后树状数组就差不多了，剩下的线段树那讲。

Addition. Tricks

动态开点

其实就是一个存储的 Trick，在点分树里面，可能需要对每个结点都开树状数组，如果直接开是 $\Omicron(n ^ 2)$ 的空间复杂度。

这个时候，我们就可以把静态数组换成 vector，根据需要来开。

你甚至可以直接继承 vector<int> 来封装一个动态开点树状数组。

线性建树

因为树状数组管辖的是 $[x - lowbit(x) + 1,x]$ 的信息，所以我们可以预处理前缀数组 $sum$ ，然后用 $sum$ 来计算树状数组每一个位置的值。

树状数组套树

如果你学过主席树，那你应该知道，线段树是可以进行前缀和的。

能方便的维护前缀和的数据结构有什么？树状数组！

具体就是树状数组每个结点存的是你需要的一种树，修改就像普通树状数组一样，在对应点位修改。

查询可以先把所有的根结点存下来，然后在内层树操作的时候同时操作所有结点。

里面什么都能套，个人经验：里面套线段树空间开销会大一点，套平衡树时间开销会大一点。

维护后缀的树状数组

可以直接把普通树状数组的修改和查询的枚举方式互换一下。

Thanks for reading!