数据结构Part 2

Wed Jan 08 2025

37 minutes

6607 words

这玩意会持续更新，因为太多了。

0.定义#

线段树是一种可以很方便的维护区间信息的 DS，是一种Leafy Tree。

线段树的一个节点是维护的原序列的一段区间的信息。具体结构是一棵完全二叉树，若一个节点维护的是 $[l,r]$ 的信息，设 $m = \lfloor \frac{l + r}{2} \rfloor$ 则根节点的左儿子维护的就是 $[l,m]$ ，右儿子维护的是 $[m + 1,r]$ 的信息。

节点需要用 pushup 操作来合并信息，由于是分两块计算，所以维护的东西必须有结合律，更准确的说，维护的信息必须是个幺半群，即需要有结合律，有单位元。

一般设根节点的下标为 rt，则左子树的下标为 rt * 2 = rt << 1，右子树的下标为 rt * 2 + 1 = rt << 1 | 1。

结构体如下：

CPP

struct Rukkhadevata
{
    int l,r;
    Info...;
    // Lazytag...;
}tree[MAXN << 2];
inline void pushup(int rt)
{
    tree[rt].info = merge(tree[rt << 1].info,tree[rt << 1 | 1].info);
}
inline void pushdown(int rt)
{
    if(available(tree[rt].laz))
    {
        Operation(rt << 1,tree[rt].laz);
        Operation(rt << 1 | 1,tree[rt].laz);
        reset(tree[rt].laz);
    }
}

需要注意，这种堆式存储要开 4 倍空间。

1.操作#

建树#

我们递归的处理每个区间，对每个节点分配边界，如果是叶子节点就分配信息，在回溯的时候执行 pushup 合并信息。

CPP

inline void build(int l,int r,int rt)
{
    tree[rt].l = l,tree[rt].r = r;
    if(l == r)
    {
        tree[rt].info = origin[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build(l,mid,rt << 1);
    build(mid + 1,r,rt << 1 | 1);
    pushup(rt);
}

区间修改类#

我们需要维护一个 lazytag，具体的，就是直接给一个子树的根节点打标记，不直接修改，等需要查询子区间的时候再 pushdown 下去。不同的 lazytag 间可能相互有影响，需要根据维护的信息适时下放标记。

然后我们需要递归区间，分三种情况：

修改区间完全包含现区间，则直接打标记。
修改区间和现区间的左半部分有交集，就递归向左子树走。
修改区间和现区间的右半部分有交集，就递归向右子树走。

模板代码如下：

CPP

inline void modify(int l,int r,int rt,int val)
{
    if(l <= tree[rt].l && r >= tree[rt].r)
    {
        Operation(rt,val);
        return ;
    }
    // pushdown(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if(l <= mid)
        modify(l,r,rt << 1,val);
    if(r > mid)
        modify(l,r,rt << 1 | 1,val);
    pushup(rt);
}

区间查询类#

还是一样的，注意准备前往子节点的时候需要下传标记。

CPP

inline int query(int l,int r,int rt)
{
    if(l <= tree[rt].l && r >= tree[rt].r)
        return tree[rt].val;
    // pushdown(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1,res = identity();
    if(l <= mid)
        Operation(res,query(l,r,rt << 1));
    if(r > mid)
        Operation(res,query(l,r,rt << 1 | 1));
    return res;
}

2.权值线段树#

类似权值树状数组，可以查询全局 $k$ 小值，查询排名等，在某些时候可以代替平衡树。

$k$ 小值可以线段树上二分，排名就是直接一个前缀和。

3.动态开点线段树#

有的时候，题目不允许我们使用堆式存储开线段树，又不能离散化的时候，我们就可以使用动态开点的方式。具体的，就是刚开始只有一个管辖 $[1,n]$ 的根节点，等需要用的时候才开这个点。

因为每次操作最多创建 $\Omicron(\log n)$ 个节点，所以最后的空间复杂度可以从 $T(4n)$ 优化到 $\Omicron(q \log n)$ 。

结构体会有些变化：

CPP

struct Rukkhadevata
{
    int ls,rs;
    int l,r; // 其实可以不计
    Info...;
    // Lazytag...;
}tree[MAXQ * LOGN];
#define lson tree[rt].ls
#define rson tree[rt].rs

需要多加一个 newNode 操作，你也可以选择不加。~~这怎么一股平衡树味~~

CPP

inline int newNode(int l,int r,int val)
{
    ++cnt;
    tree[cnt].l = l,tree[cnt].r = r,tree[cnt].val = val,tree[cnt].ls = tree[cnt].rs = 0;
    return cnt;
}

因为不需要初始化所有节点，所以我们可以省略建树操作。相应的，别的操作也需要一些修改。

CPP

inline void pushup(int rt)
{
    tree[rt].val = merge(tree[lson].val,tree[rson].val);
}
inline void pushdown(int rt)
{
    if(tree[rt].laz)
    {
        if(lson)
            Operation(lson,tree[rt].laz);
        if(rson)
            Operation(rson,tree[rt].laz);
        reset(tree[rt].laz);
    }
}
inline void modify(int &rt,int l,int r,int L,int R,int val)
{
    if(!rt)
        rt = newNode(l,r,val);
    if(L <= l && R >= r)
    {
        Operation(rt,val);
        return ;
    }
    int mid = (l + r) >> 1;
    if(L <= mid)
        modify(lson,l,mid,L,R,val);
    if(R > mid)
        modify(rson,mid + 1,r,L,R,val);
    pushup(rt);
}
inline int query(int rt,int l,int r,int L,int R)
{
    if(!rt)
        return 0;
    if(L <= l && R >= r)
        return tree[rt].val;
    int mid = (l + r) >> 1,res = identity();
    if(L <= mid)
        Operation(res,query(lson,l,mid,L,R));
    if(R > mid)
        Operation(res,query(rson,mid + 1,r,L,R));
    return res;
}

4.势能线段树#

lazytag 的需求就是可以合并，并且可以更新子节点。但是有的操作就不满足，比如区间开根。

但是，我们惊奇的发现，区间开根对 $0$ 和 $1$ 没有贡献。所以，我们可以维护区间最大值，若最大值 $\le 1$ 则直接返回，否则接着向下走。

也因此，我们可以维护区间历史最值，区间取 min/max 等操作，而这就是吉司机线段树。

5.李超线段树#

~~这是真“线段”树~~

这个线段树是用来维护线段的最高/最低点的，并且可以支持插入线段。

每个节点维护的是一段区间内的最优线段，就是这个线段在区间中点处的 $y$ 值是最大的线段。

这个东西的核心就在分类讨论，具体如下：

新线段完全覆盖老线段，则直接修改，返回。
老线段完全覆盖新线段，则直接返回。
刚好交于中点，归于新线段不如老线段。
这写不下，往下看。

如果新线段 $f$ 优于老线段 $g$ ，就先交换一下，我们考虑中点处 $f$ 不如 $g$ 优的情况。

若左端点 $f$ 优于 $g$ ，则交点会在左区间，前往左儿子处理。
若右端点 $f$ 优于 $g$ ，则交点会在右区间，前往右儿子处理。
如果都不优，则直接返回。

或者还有一种比较斜率的办法：

若 $g$ 的斜率小于 $f$ ，则比较中点的 $y$ 坐标，若 $g$ 小于 $f$ 则前往右儿子更新 $g$ ，否则前往左儿子更新 $f$ 。
若 $g$ 的斜率大于 $f$ ，且中点坐标 $g$ 小于 $f$ ，则前往左儿子更新 $g$ ，否则前右儿子更新 $f$ 。
斜率一致那比较截距， $f$ 优于 $g$ 就更新。

查询就很简单，枚举所有可能包含 $pos$ 的线段，然后取极值。

模板代码如下（不含线段拆分，给斜率优化用的那种）：

CPP

namespace LiChaoSGT
{
    struct Rukkhadevata
    {
        int ls,rs,seg;
    }tree[MAXN];
    int k[MAXN],b[MAXN];
    inline int F(int id,int x)
    {return k[id] * x + b[id];}
    int cnt,root;
    inline void insert(int &rt,int l,int r,int S)
    {
        if(!rt)
            tree[rt = ++cnt].seg = S;
        else
        {
            if(l == r)
            {
                if(F(S,l) < F(tree[rt].seg,l))
                    tree[rt].seg = S;
                return ;
            }
            int mid = (l + r) >> 1;
            if(F(S,mid) < F(tree[rt].seg,mid))
                swap(S,tree[rt].seg);
            if(F(S,l) < F(tree[rt].seg,l))
                insert(tree[rt].ls,l,mid,S);
            if(F(S,r) < F(tree[rt].seg,r))
                insert(tree[rt].rs,mid + 1,r,S);
        }
    }
    inline int query(int rt,int l,int r,int p)
    {
        if(!rt)
            return LONG_LONG_MAX;
        if(l == r)
            return F(tree[rt].seg,p);
        int mid = (l + r) >> 1;
        return min(F(tree[rt].seg,p),(p <= mid) ? query(tree[rt].ls,l,mid,p) : query(tree[rt].rs,mid + 1,r,p));
    }
}

6.可持久化#

这玩意分两种，但维护都差不多（我感觉可持久化数据结构的变化都挺像的）

可持久化线段树#

我喜欢叫可持久化数组。

我们先思考，怎么暴力可持久化。

这不简单，直接复制

是，但是空间立刻爆炸。

我们发现，每次修改，最多会访问 $\log n$ 个节点，如下图：

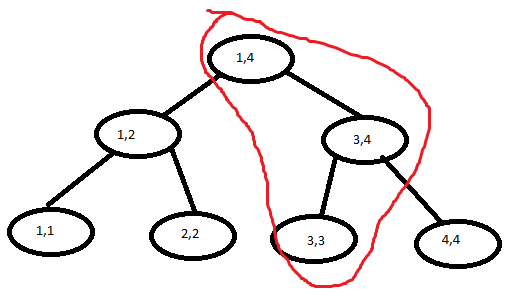
所以，我们可以考虑只将这一条链复制下来，和原来的线段树共用一些节点，对每个版本，把根节点存下来就好了。

其实懂了以后就不难写出代码，这里贴一个模板题的：

CPP

namespace PersistentSGT
{
    struct Nahida
    {
        int ls,rs,val;
    }tree[MAXN << 5];
    int cnt,root[MAXN];
    inline int newNode(int node)
    {
        ++cnt;
        tree[cnt] = tree[node];
        return cnt;
    }
    inline int build(int rt,int l,int r)
    {
        rt = ++cnt;
        if(l == r)
        {
            tree[rt].val = a[l];
            return cnt;
        }
        int mid = (l + r) >> 1;
        tree[rt].ls = build(tree[rt].ls,l,mid);
        tree[rt].rs = build(tree[rt].rs,mid + 1,r);
        return rt;
    }
    inline int update(int rt,int l,int r,int pos,int val)
    {
        rt = newNode(rt);
        if(l == r)
            tree[rt].val = val;
        else
        {
            int mid = (l + r) >> 1;
            if(pos <= mid)
                tree[rt].ls = update(tree[rt].ls,l,mid,pos,val);
            else
                tree[rt].rs = update(tree[rt].rs,mid + 1,r,pos,val);
        }
        return rt;
    }
    inline int query(int rt,int l,int r,int pos)
    {
        if(l == r)
            return tree[rt].val;
        int mid = (l + r) >> 1;
        if(pos <= mid)
            return query(tree[rt].ls,l,mid,pos);
        else
            return query(tree[rt].rs,mid + 1,r,pos);
    }
}

可持久化权值线段树#

也叫主席树。

就是把权值线段树可持久化的产物，可以拿来解决区间 k 小值。

具体来说，先离散化，然后从左到右依次添加每个值，并且每次添加完后保存根节点，这样我们就得出了所有 $[1,i]$ 的线段树，这个时候，我们可以运用差分的思想，用 $[1,r]$ 的线段树减去 $[1,l - 1]$ 的线段树（每个节点对应相减），就得到了 $[l,r]$ 的线段树。然后正常权值线段树查询 $k$ 小值就行了。

应用#

可持久化线段树可以让很多基于数组的数据结构变得可持久化，还有就是维护每次变化很小并且需要访问历史版本的信息。

主席树用处就多了去了，外层的前缀和/差分可以看作一层数据结构，因此主席树维护的是静态的二维信息，你可以把外面的换成树状数组，就可以维护动态的了。

同时，这个启发我们，权值线段树是可以“差分”的。

虽然说不强制在线可以被整体二分/CDQ 分治等离线算法吊着打，~~但是我就喜欢 DS~~。

注意#

但凡是可持久化的题空间一般不会太小，除非毒瘤出题人。所以我们可以大胆一点，直接开 $32$ 倍空间。

并且这个东西需要共用节点，不能写堆式存储，必须写动态开点的写法。

类似的前缀和思想在可持久化字典树也有体现。

7.标记永久化#

有的时候，上面的上传/下传标记不再适用，比如写主席树和树套树的时候。

这个时候，我们干脆直接不下传标记，直接在访问某个节点的时候累加所有标记就行了。

修改会有些不同：如果操作区间完全覆盖现在的区间，则只打标记不改值，否则修改值。

可以看下面的模板，实现了区间加法：

CPP

#include <bits/stdc++.h>
#define int long long
using namespace std;

constexpr int MAXN = 1e5 + 24;
struct Rukkhadevata
{
    int val,laz;
}tree[MAXN << 2];
int a[MAXN];
inline void build(int l,int r,int rt)
{
    if(l == r)
    {
        tree[rt].val = a[l];
        return ;
    }
    int mid = (l + r) >> 1;
    build(l,mid,rt << 1);
    build(mid + 1,r,rt << 1 | 1);
    tree[rt].val = tree[rt << 1].val + tree[rt << 1 | 1].val; // 建树需要 pushup 一下
}
inline void modify(int rt,int l,int r,int L,int R,int val)
{
    if(L <= l && R >= r)
    {
        tree[rt].laz += val; // 完全覆盖只打标记
        return ;
    }
    tree[rt].val += (R - L + 1) * val; // 否则修改值
    int mid = (l + r) >> 1;
    if(R <= mid)
        modify(rt << 1,l,mid,L,R,val);
    else if(L > mid)
        modify(rt << 1 | 1,mid + 1,r,L,R,val);
    else
        modify(rt << 1,l,mid,L,mid,val),modify(rt << 1 | 1,mid + 1,r,mid + 1,R,val);
}
inline int query(int rt,int l,int r,int L,int R)
{
    int res = tree[rt].laz * (R - L + 1); // 累加标记的贡献
    if(L <= l && R >= r)
        return tree[rt].val + res;
    int mid = (l + r) >> 1;
    if(R <= mid)
        res += query(rt << 1,l,mid,L,R);
    else if(L > mid)
        res += query(rt << 1 | 1,mid + 1,r,L,R);
    else
        res += query(rt << 1,l,mid,L,mid) + query(rt << 1 | 1,mid + 1,r,mid + 1,R);
    return res;
}
int n,m,opt,l,r,v;
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin >> n >> m;
    for(int i = 1;i <= n;i++)
        cin >> a[i];
    build(1,n,1);
    for(int i = 1;i <= m;i++)
    {
        cin >> opt >> l >> r;
        if(opt == 1)
        {
            cin >> v;
            modify(1,1,n,l,r,v);
        }
        else
            cout << query(1,1,n,l,r) << "\n";
    }
}

8.线段树维护矩阵乘法#

前面我们说了，线段树维护的信息实质上是一个幺半群。

我们又发现，矩阵乘法这东西既有结合律还有单位元，所以可以放到线段树上维护。

但直接维护，显然没有什么意义，除非有毒瘤出题人出这个可爱题。

我们回过头去看P3373 线段树2，发现我们需要维护两个 lazytag，太烦了。

这个时候，我们维护的矩阵乘法就有用了。

我们不难发现，我们可以~~多此一举的~~做下面的操作：

$a \gets a + k \Rightarrow \begin{bmatrix} a \end{bmatrix} \gets \begin{bmatrix} a \end{bmatrix} + \begin{bmatrix} k \end{bmatrix}$

然后，对于线段树的每个节点，我们考虑维护一个矩阵 $\begin{bmatrix} val & len \end{bmatrix}$ ，其中 $val$ 表示这个节点的值， $len$ 表示该区间长度。

我们不难构造出这个转移矩阵 $\begin{bmatrix} 1 & 0 k & 1 \end{bmatrix}$ ，使得我们可以将加法操作写成 $\begin{bmatrix} val & len \end{bmatrix} \gets \begin{bmatrix} val & len \end{bmatrix} \begin{bmatrix} 1 & 0 k & 1 \end{bmatrix}$ 。

同理，我们可以构造出一个乘法的转移矩阵 $\begin{bmatrix} k & 0 0 & 1 \end{bmatrix}$ 。

这个时候，我们矩阵乘法的结合律就发挥作用了。我们只用维护一个矩阵作为 lazytag，就可以了。

但是，它的作用远不止于此。

我们可以定义广义矩阵乘法如下：

C = A * B C _ {i,j} = \max A _ {i,k} + B _ {k,j}

懒得证明了，反正它有结合律，还有单位元为 $\begin{bmatrix} 0 & -\infty & \ldots & -\infty -\infty & 0 & \ldots & -\infty \vdots & \vdots & \ddots & \vdots -\infty & -\infty & \ldots & 0 \end{bmatrix}$ 。

我们再看这道题：P4314 CPU 监控。

我们可以将信息这么维护： $\begin{bmatrix} a _ i & b _ i & 0 \end{bmatrix}$ ， $a _ i$ 表示这个位置的值， $b _ i$ 表示历史最值。pushup 就是维护区间最值， $a _ i \gets \max \{ a _ {ls _ i},a _ {rs _ i} \},b _ i \gets \max \{ b _ {ls _ i},b _ {rs _ i} \}$ 。

因为 $\begin{bmatrix} a _ i & b _ i & 0 \end{bmatrix} \to \begin{bmatrix} a _ i + k & \max \{b _ i,a _ i + k\} & 0 \end{bmatrix}$ ，加法矩阵是长这样的： $\begin{bmatrix} k & k & -\infty -\infty & 0 & -\infty -\infty & -\infty & 0 \end{bmatrix}$ ； $\begin{bmatrix} a _ i & b _ i & 0 \end{bmatrix} \to \begin{bmatrix} k & \max \{b _ i,k\} & 0 \end{bmatrix}$ ，覆盖矩阵是 $\begin{bmatrix} -\infty & -\infty & -\infty -\infty & 0 & -\infty k & k & 0 \end{bmatrix}$ 。

然后就可以方便的维护这些操作了。

~~但是两个大常数的东西在一起真的不会 T 吗~~

这个东西可能需要一些卡常，可以用标记永久化降低常数。

动态 DP 也是基于这个原理，可以用数据结构维护。

9.吉司机线段树/Segment Beats#

可以维护区间取最值操作/区间历史最值查询。

先上一道例题

给你一个序列 $a _ i$ ，维护以下操作
$\forall i \in [l,r],a _ i \gets \min (a _ i,x)$
输出 $\max \{ a _ i \},i \in [l,r]$
输出 $\sum _ {i = l} ^ r a _ i$

我们发现取 $\min$ 很不好维护，考虑转化。

我们维护以下几个值：

区间内最大值 $max$ ，区间内严格次大值 $smx$ ，区间和 $sum$ ，区间内最大值个数 $cnt$ 。

再维护以下 lazytag：

加法标记 $lazsum$ ，取 $\min$ 标记 $lazmin$

我们考虑将取 $\min$ 操作转化为加减法。

对于操作 $1$ ，做以下分类讨论：

若 $x \ge max$ ，则操作对这个区间及子区间无效，直接返回（和上面的势能线段树类似）。
若 $smx \lt x \le max$ ，操作会对所有的 $max$ 生效，对区间和产生 $(x - max)cnt$ 的贡献，同时打标记。
否则，暴力向下。

这个可以通过势能分析法证明，复杂度是 $\Omicron(n \log n)$ 的。

有些题会让你同时维护六个操作（区间 $\min / \max / \sum$ 修改/查询），这种出生题码量会非常大，同时需要大力分讨。

所以吉司机线段树一个 pushup 有 $40$ 多行挺正常的。

这里附一份完整代码。

BZOJ 4695，上面的六个操作的

CPP

#include <bits/stdc++.h>
#define int long long
using namespace std;

constexpr int MAXN = 5e5 + 5,inf = 1e18;
int n,m,opt,l,r,x,a[MAXN];
struct Rukkhadevata
{
    int max,min,smx,smn,mxCnt,mnCnt,sum;
    int lazmx,lazmn,lazsm;
}tree[MAXN << 2];
inline void pushup(int rt)
{
    tree[rt].sum = tree[rt << 1].sum + tree[rt << 1 | 1].sum;
    if(tree[rt << 1].max == tree[rt << 1 | 1].max)
    {
        tree[rt].max = tree[rt << 1].max;
        tree[rt].smx = max(tree[rt << 1].smx,tree[rt << 1 | 1].smx);
        tree[rt].mxCnt = tree[rt << 1].mxCnt + tree[rt << 1 | 1].mxCnt;
    }
    else if(tree[rt << 1].max > tree[rt << 1 | 1].max)
    {
        tree[rt].max = tree[rt << 1].max;
        tree[rt].smx = max(tree[rt << 1].smx,tree[rt << 1 | 1].max);
        tree[rt].mxCnt = tree[rt << 1].mxCnt;
    }
    else
    {
        tree[rt].max = tree[rt << 1 | 1].max;
        tree[rt].smx = max(tree[rt << 1].max,tree[rt << 1 | 1].smx);
        tree[rt].mxCnt = tree[rt << 1 | 1].mxCnt;
    }
    if(tree[rt << 1].min == tree[rt << 1 | 1].min)
    {
        tree[rt].min = tree[rt << 1].min;
        tree[rt].smn = min(tree[rt << 1].smn,tree[rt << 1 | 1].smn);
        tree[rt].mnCnt = tree[rt << 1].mnCnt + tree[rt << 1 | 1].mnCnt;
    }
    else if(tree[rt << 1].min < tree[rt << 1 | 1].min)
    {
        tree[rt].min = tree[rt << 1].min;
        tree[rt].smn = min(tree[rt << 1].smn,tree[rt << 1 | 1].min);
        tree[rt].mnCnt = tree[rt << 1].mnCnt;
    }
    else 
    {
        tree[rt].min = tree[rt << 1 | 1].min;
        tree[rt].smn = min(tree[rt << 1].min,tree[rt << 1 | 1].smn);
        tree[rt].mnCnt = tree[rt << 1 | 1].mnCnt;
    }
}
inline void build(int l,int r,int rt)
{
    tree[rt].lazmn = inf,tree[rt].lazmx = -inf;
    if(l == r)
    {
        tree[rt].sum = tree[rt].max = tree[rt].min = a[l];
        tree[rt].smx = -inf,tree[rt].smn = inf;
        tree[rt].mxCnt = tree[rt].mnCnt = 1;
        return ;
    }
    int mid = (l + r) >> 1;
    build(l,mid,rt << 1);
    build(mid + 1,r,rt << 1 | 1);
    pushup(rt);
}
inline void updateSum(int rt,int val,int l,int r)
{
    tree[rt].sum += (r - l + 1ll) * val;
    tree[rt].max += val,tree[rt].min += val;
    if(tree[rt].lazmn != inf)
        tree[rt].lazmn += val;
    if(tree[rt].lazmx != -inf)
        tree[rt].lazmx += val;
    if(tree[rt].smn != inf)
        tree[rt].smn += val;
    if(tree[rt].smx != -inf)
        tree[rt].smx += val;
    tree[rt].lazsm += val;
}
inline void updateMin(int rt,int val)
{
    if(tree[rt].max <= val)
        return ;
    tree[rt].sum += (val - tree[rt].max) * tree[rt].mxCnt;
    if(tree[rt].smn == tree[rt].max)
        tree[rt].smn = val;
    if(tree[rt].min == tree[rt].max)
        tree[rt].min = val;
    tree[rt].lazmx = min(tree[rt].lazmx,val),tree[rt].max = val,tree[rt].lazmn = val;
}
inline void updateMax(int rt,int val)
{
    if(tree[rt].min > val)
        return ;
    tree[rt].sum += (val - tree[rt].min) * tree[rt].mnCnt;
    if(tree[rt].smx == tree[rt].min)
        tree[rt].smx = val;
    if(tree[rt].max == tree[rt].min)
        tree[rt].max = val;
    tree[rt].lazmn = max(tree[rt].lazmn,val),tree[rt].min = val,tree[rt].lazmx = val;
}
inline void pushdown(int rt,int l,int r)
{
    int mid = (l + r) >> 1;
    if(tree[rt].lazsm)
    {
        updateSum(rt << 1,tree[rt].lazsm,l,mid);
        updateSum(rt << 1 | 1,tree[rt].lazsm,mid + 1,r);
        tree[rt].lazsm = 0;
    }
    if(tree[rt].lazmx != -inf)
    {
        updateMax(rt << 1,tree[rt].lazmx);
        updateMax(rt << 1 | 1,tree[rt].lazmx);
        tree[rt].lazmx = -inf;
    }
    if(tree[rt].lazmn != inf)
    {
        updateMin(rt << 1,tree[rt].lazmn);
        updateMin(rt << 1 | 1,tree[rt].lazmn);
        tree[rt].lazmn = inf;
    }
}
inline void modifySum(int rt,int l,int r,int L,int R,int val)
{
    if(L <= l && R >= r)
        return updateSum(rt,val,l,r);
    pushdown(rt,l,r);
    int mid = (l + r) >> 1;
    if(L <= mid)
        modifySum(rt << 1,l,mid,L,R,val);
    if(R > mid)
        modifySum(rt << 1 | 1,mid + 1,r,L,R,val);
    pushup(rt);
}
inline void modifyMin(int rt,int l,int r,int L,int R,int val)
{
    if(tree[rt].max <= val)
        return ;
    if(L <= l && R >= r && tree[rt].smx < val)
        return updateMin(rt,val);
    pushdown(rt,l,r);
    int mid = (l + r) >> 1;
    if(L <= mid)
        modifyMin(rt << 1,l,mid,L,R,val);
    if(R > mid)
        modifyMin(rt << 1 | 1,mid + 1,r,L,R,val);
    pushup(rt);
}
inline void modifyMax(int rt,int l,int r,int L,int R,int val)
{
    if(tree[rt].min >= val)
        return ;
    if(L <= l && R >= r && tree[rt].smn > val)
        return updateMax(rt,val);
    pushdown(rt,l,r);
    int mid = (l + r) >> 1;
    if(L <= mid)
        modifyMax(rt << 1,l,mid,L,R,val);
    if(R > mid)
        modifyMax(rt << 1 | 1,mid + 1,r,L,R,val);
    pushup(rt);
}
inline int querySum(int rt,int l,int r,int L,int R)
{
    if(L <= l && R >= r)
        return tree[rt].sum;
    pushdown(rt,l,r);
    int mid = (l + r) >> 1,res = 0;
    if(L <= mid)
        res += querySum(rt << 1,l,mid,L,R);
    if(R > mid)
        res += querySum(rt << 1 | 1,mid + 1,r,L,R);
    return res;
}
inline int queryMax(int rt,int l,int r,int L,int R)
{
    if(L <= l && R >= r)
        return tree[rt].max;
    pushdown(rt,l,r);
    int mid = (l + r) >> 1,res = -inf;
    if(L <= mid)
        res = max(res,queryMax(rt << 1,l,mid,L,R));
    if(R > mid)
        res= max(res,queryMax(rt << 1 | 1,mid + 1,r,L,R));
    return res;
}
inline int queryMin(int rt,int l,int r,int L,int R)
{
    if(L <= l && R >= r)
        return tree[rt].min;
    pushdown(rt,l,r);
    int mid = (l + r) >> 1,res = inf;
    if(L <= mid)
        res = min(res,queryMin(rt << 1,l,mid,L,R));
    if(R > mid)
        res = min(res,queryMin(rt << 1 | 1,mid + 1,r,L,R));
    return res;
}
signed main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin >> n;
    for(int i = 1;i <= n;i++)
        cin >> a[i];
    build(1,n,1);
    cin >> m;
    while(m--)
    {
        cin >> opt >> l >> r;
        if(opt == 1)
        {
            cin >> x;
            modifySum(1,1,n,l,r,x);
        }
        if(opt == 2)
        {
            cin >> x;
            modifyMax(1,1,n,l,r,x);
        }
        if(opt == 3)
        {
            cin >> x;
            modifyMin(1,1,n,l,r,x);
        }
        if(opt == 4)
            cout << querySum(1,1,n,l,r) << '\n';
        if(opt == 5)
            cout << queryMax(1,1,n,l,r) << '\n';
        if(opt == 6)
            cout << queryMin(1,1,n,l,r) << '\n';
    }
}

~~太 nm 长了~~

Seg Beats 其实不止可以给线段树用，它实际上是一种把区间最值操作转化为区间加减的 Trick，因此，面对带插入的问题，你甚至可以在平衡树上跑这个东西，~~只是代码还能再多 100 多行~~。

10.线段树合并#

就是把两棵线段树所维护的信息合并起来。

显然，静态的线段树合并没有什么实际意义，最好的方法就是全部拉出来重构。

所以我们常常是合并动态开点的线段树。

过程和 FHQ Treap 差不多，如果遇到 $A$ 树中有一个节点而 $B$ 树中没有，则直接返回这个节点。

如果已经递归到叶子节点，就合并他们的信息（就是对两个叶子节点进行一次维护的操作），然后返回。

代码分在线和离线两种。

先讲离线的，就是直接将 $B$ 树的信息合并到 $A$ 树中。但是后面就不能有修改操作了，否则会导致信息错乱。

代码很简单：

CPP

inline int merge(int L,int R,int l,int r)
{
    if(!L || !R)
        return L | R;
    if(l == r)
    {
        tree[L].mx += tree[R].mx;
        tree[L].maxid = l;
        return L;
    }
    int mid = (l + r) >> 1;
    lson(L) = merge(lson(L),lson(R),l,mid);
    rson(L) = merge(rson(L),rson(R),mid + 1,r);
    pushup(L);
    return L;
}

在线的做法就是每次合并就新开一个点，把两棵线段树的信息都合并进去，缺点就是空间占用太大了。

11.线段树分裂#

对于一个无序的序列，分裂显然没有什么用，所以我们一般分裂的是权值线段树。

时刻记住，线段树是 Leafy Tree，所以单独一个区间会分裂出来一条链。

但是我觉得这玩意好像考的很少，感觉还是合并会多一点。

具体操作就先分三类讨论：

现在的区间和分裂区间无交集：直接返回
现在的区间和分裂区间有交集：新建节点，往子节点走
被完全包含：断开原有的边，接到新树下方

~~我感觉这两个和 FHQ Treap 好像啊~~

12.线段树优化建图#

虽然连边是 $\Omicron(1)$ 的无法优化了，但是有的时候，边的数量会很多，这个时候就该优化建图了。

线段树可以处理 $[l1,r1](l1 \le r1)$ 向 $[l2,r2](l2 \le r2)$ 连边的问题，这个区间可以是单点。

我们构建两个线段树，叶子节点是给你的点，第一棵从父亲向儿子连边，叫做出树，第二棵从儿子连向父亲，叫做入树。两棵树可以共用叶子节点，也可以分别建，再从出树到入树对应连边。

这些点都是多加的虚点，注意在跑图论算法的时候不要计入贡献。

分几种情况：

(1) 单点连单点#

~~直接连不就是了吗。~~

(2) 单点连区间#

我们在入树中找到单点，再将连的区间按照线段树的套路拆成出树上的 $\Omicron(\log n)$ 个区间，然后单点连向拆分出的区间。

(3) 区间连单点#

把上面的出入反一下。

(4) 区间连区间#

我们新建一个虚点 $p$ ，同样的拆分区间。入树中的点连向 $p$ ， $p$ 再连向出树中的点。

可以发现，边的数量是 $\Omicron(n \log n)$ 的，时间复杂度可以优化为 $\Omicron(n \log n)$ 。

13.线段树分治#

我觉得这个东西还不如叫时间分治，只是有区间操作用线段树维护会更快一点。

实际上就是一个操作，直接操作是容易的，但是难以删除，并且对时间轴上的一个区间生效，那我们就可以按照线段树的方式拆分区间，在 $\log n$ 个区间上打上标记，并在叶子节点计算答案。

实现上，我们线段树每个节点是一个 vector，存储这个节点该加入的操作。我们先添加操作，然后遍历整棵线段树，进入一个节点就加入所有操作，遍历到叶子节点的时候返回答案，离开一个节点就撤销加入的操作。

因此，我们就可以维护出现的时间，将定点删除操作转化为撤销操作。维护你需要的操作还需要其他东西，比如线性基，并查集等，并且你得考虑是否能方便的撤销。

Addition.一些小 Tricks#

线段树维护操作序列#

就是把操作序列抽象成普通序列，然后放到线段树上维护。

只要这个操作序列可以抽象成幺半群，那就可以用线段树维护。

Eg. Luogu P4588

我们用线段树维护区间乘积，对于 $1$ 操作，把 $i$ 处的值修改为 $x$ ，对于 $2$ 操作，把 $x$ 处的值修改为 $1$ 。

查询都可以不写，直接求 tree[root] 处的值就好了。

二维偏序 & 树套树#

因为本人不太喜欢 CDQ 分治，所以决定在这里就写二维偏序。

如果是离线的二维数点，我们可以直接扫描线 + 树状数组来解决，如果值域太大，也可以用主席树解决，离散化后对每一个横坐标新建一个版本并进行更改。查询可以直接用主席树惯用套路，用右横坐标的版本减去左横坐标的前一个版本来构建区间的树，然后在上面跑纵坐标的区间查询就行。

但是放到动态呢？你可以说加个时间维度，跑三维偏序，~~但我就喜欢用纯 DS~~。

我们可以用树套树维护这个，外层树可以是树状数组这种方便查询前缀的 DS，开不下可以换成线段树，内层一般不会让你开下第二个树状数组，于是我们可以选择权值树状数组或者平衡树。

两个做比较的话，就是里面放线段树的空间会大一点，平衡树的时间会大一点。

然后线段树同样可以作为外层树，但是就必须对整条链进行操作，不能打标记。

卡常#

这里会放一些我常用的卡常小技巧。

可以离线的话，权值线段树可以先进行一遍离散化，可以把单次 $\log V$ 变为 $\log n$ 。

如果是单点操作的话，修改可以不写 pushup/pushdown，直接一路修改下去。

数据结构Part 2

https://blog.xguagua.cfd/blog/数据结构p2/